Plotting
Bézier curves
Challenge
Math Links

Plotting

  1. Download member dnewman's 3dplot.scad and place it in the same directory as your OpenSCAD file that will use it.

  2. Create a new OpenSCAD document. Save it as 2dgraphing.scad. Paste this code, which is derived from user Brad Pitcher, into the empty document: 
    pi = 3.1415926536;
e = 2.718281828;

/*************************
* Cartesian equations 
*************************/
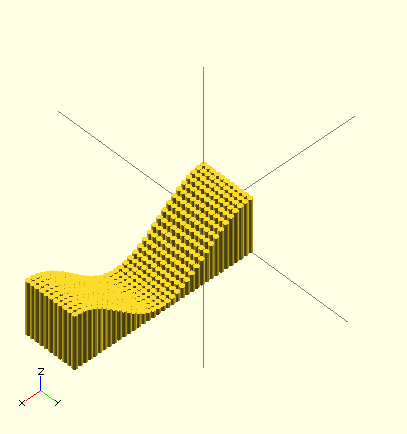
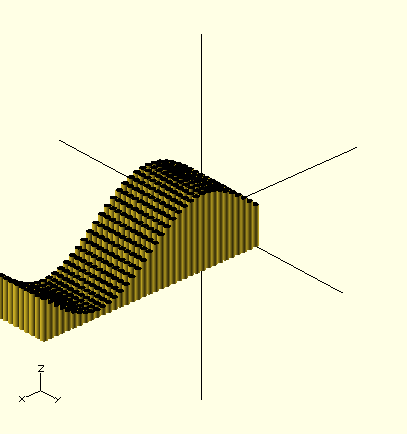
/* Sine wave */

module sineWave(){
    linear_extrude(height=5)
    2dgraph([-50, 50], 3, steps=50);
}

module  parabola (){
    linear_extrude(height=5)
    2dgraph([-50, 50], 3, steps=40);
}

/* Ellipsoid - use a cartesion equation for a half ellipse, 
then rotate extrude it */

module ellipsoid(){

    rotate_extrude(convexity=10, $fn=100) 
    rotate([0, 0, -90]) 
    2dgraph([-50, 50], 3, steps=100);
}

/*************************
* Polar equations 
*************************/
/* Rose curve */

module rose(){
    scale([20, 20, 20]) linear_extrude(height=0.15)
    2dgraph([0, 720], 0.1, steps=160, polar=true);
}

/* Archimedes spiral */
module archimedesSpiral(){
    scale([0.02, 0.02, 0.02]) linear_extrude(height=150)
    2dgraph([0, 360*3], 50, steps=100, polar=true);
}

/* Golden spiral */
module goldenSpiral(){
    linear_extrude(height=50)
    2dgraph([0, 7*180], 1, steps=300, polar=true);
}

/**************************
* Parametric equations 
*************************/
/* 9-pointed star */
module ninePointedStar(s,h){
    scale(s) linear_extrude(height=h)
    2dgraph([10, 1450], 0.1, steps=9, parametric=true);
}

/*************************/
// function to convert degrees to radians
function d2r(theta) = theta*360/(2*pi);

// These functions are here to help get the slope of each segment, and use that to find points for a correctly oriented polygon
function diffx(x1, y1, x2, y2, th) = cos(atan((y2-y1)/(x2-x1)) + 90)*(th/2);
function diffy(x1, y1, x2, y2, th) = sin(atan((y2-y1)/(x2-x1)) + 90)*(th/2);
function point1(x1, y1, x2, y2, th) = [x1-diffx(x1, y1, x2, y2, th), y1-diffy(x1, y1, x2, y2, th)];
function point2(x1, y1, x2, y2, th) = [x2-diffx(x1, y1, x2, y2, th), y2-diffy(x1, y1, x2, y2, th)];
function point3(x1, y1, x2, y2, th) = [x2+diffx(x1, y1, x2, y2, th), y2+diffy(x1, y1, x2, y2, th)];
function point4(x1, y1, x2, y2, th) = [x1+diffx(x1, y1, x2, y2, th), y1+diffy(x1, y1, x2, y2, th)];
function polarX(theta) = cos(theta)*r(theta);
function polarY(theta) = sin(theta)*r(theta);

module nextPolygon(x1, y1, x2, y2, x3, y3, th) {
    if((x2 > x1 && x2-diffx(x2, y2, x3, y3, th) < x2-diffx(x1, y1, x2, y2, th) || (x2 <= x1 && x2-diffx(x2, y2, x3, y3, th) > x2-diffx(x1, y1, x2, y2, th)))) {
        polygon(
            points = [
                point1(x1, y1, x2, y2, th),
                point2(x1, y1, x2, y2, th),
                // This point connects this segment to the next
                point4(x2, y2, x3, y3, th),
                point3(x1, y1, x2, y2, th),
                point4(x1, y1, x2, y2, th)
            ],
            paths = [[0,1,2,3,4]]
        );
    }
    else if((x2 > x1 && x2-diffx(x2, y2, x3, y3, th) > x2-diffx(x1, y1, x2, y2, th) || (x2 <= x1 && x2-diffx(x2, y2, x3, y3, th) < x2-diffx(x1, y1, x2, y2, th)))) {
        polygon(
            points = [
                point1(x1, y1, x2, y2, th),
                point2(x1, y1, x2, y2, th),
                // This point connects this segment to the next
                point1(x2, y2, x3, y3, th),
                point3(x1, y1, x2, y2, th),
                point4(x1, y1, x2, y2, th)
            ],
            paths = [[0,1,2,3,4]]
        );
    }
    else {
        polygon(
            points = [
                point1(x1, y1, x2, y2, th),
                point2(x1, y1, x2, y2, th),
                point3(x1, y1, x2, y2, th),
                point4(x1, y1, x2, y2, th)
            ],
            paths = [[0,1,2,3]]
        );
    }
}

module 2dgraph(bounds=[-10,10], th=2, steps=10, polar=false, parametric=false) {

    step = (bounds[1]-bounds[0])/steps;
    union() {
        for(i = [bounds[0]:step:bounds[1]-step]) {
            if(polar) {
                nextPolygon(polarX(i), polarY(i), polarX(i+step), polarY(i+step), polarX(i+2*step), polarY(i+2*step), th);
            }
            else if(parametric) {
                nextPolygon(x(i), y(i), x(i+step), y(i+step), x(i+2*step), y(i+2*step), th);
            }
            else {
                nextPolygon(i, f(i), i+step, f(i+step), i+2*step, f(i+2*step), th);
            }
        }
    }
}
  3. Open another OpenSCAD document.

  4. To display the axes in the model view press Command+2 (MAC) or CTRL+2 (Windows and Linux).


  5. Save the new document as openscadMath.scad in the same place as you saved the other two documents.

  6. The first line of the new file should be : 
    use <2dgraph.scad>
use <3dplot.scad>


  7. This is how you would create a sine wave: 
    function _f(x) = 20*sin((1/4)*x);
function f(x) = _f(d2r(x));
sineWave();
    Press F5 to render

  8. Here are some other shapes:
    ShapeCode
    Parabola
    function f(x) = pow(x, 2)/20;
parabola();
    ellipsoid
    function f(x) = sqrt((2500-pow(x, 2))/3);
ellipsoid();
    rose
    function r(theta) = cos(4*theta);
rose();
    Archimedes Spiral
    function r(theta) = theta/2*pi;
archimedesSpiral();
    Golden Spiral
    function r(theta) = pow(e, 0.0053468*theta);
goldenSpiral();
    Nine Pointed Star
    function x(t) = cos(t);
function y(t) = sin(t);
ninePointedStar([10,10,10],0.25);


  9. For the 3d graphing there are four example graphs to play with:
    GraphCode
    Square ripples in a pond
    function z(x,y) = 2*cos(rad2deg(abs(x)+abs(y)));
3dplot([-4*pi,4*pi],[-4*pi,4*pi],[50,50],-2.5);
    A wash board
    function z(x,y) = cos(rad2deg(abs(x)+abs(y)));
3dplot([-4*pi,4*pi],[-4*pi-20,4*pi-20],[50,50],-1.1);
    Uniform bumps and dips
    function z(x,y) = 5*cos(rad2deg(x)) * sin(rad2deg(y));
3dplot([-2*pi,2*pi],[-2*pi,2*pi],[50,50],-6);
    sombrero function
    function z(x,y) = 15*cos(180*sqrt(x*x+y*y)/pi)/sqrt(2+x*x+y*y);
3dplot([-4*pi,+4*pi],[-4*pi,+4*pi],[50,50],-5);
    Select one or two, uncomment them and render the 3D graph (F5)

  10. OpenSCAD also includes syntax for for loops. Here is an example that takes advantage of the cos() function: 
    for(i=[0:36]){
    for(j=[0:10]){
        translate([i*10,j*10,0])cylinder(r=5,h=cos(i*10)*50+60);
    }
}


  11. Here is an example that takes advantage of the sin() function: 
    for(i=[0:36]){
    for(j=[0:10]){
        translate([i*10,j*10,0])cylinder(r=5,h=sin(i*10)*50+60);
    }
}